What

Brief

This is a standalone Priority Queue data structure from the data-structure-typed collection. If you wish to access more data structures or advanced features, you can transition to directly installing the complete data-structure-typed package

How

install

npm

npm i priority-queue-typed --save
Copy

yarn

yarn add priority-queue-typed
Copy

methods

Priority Queue 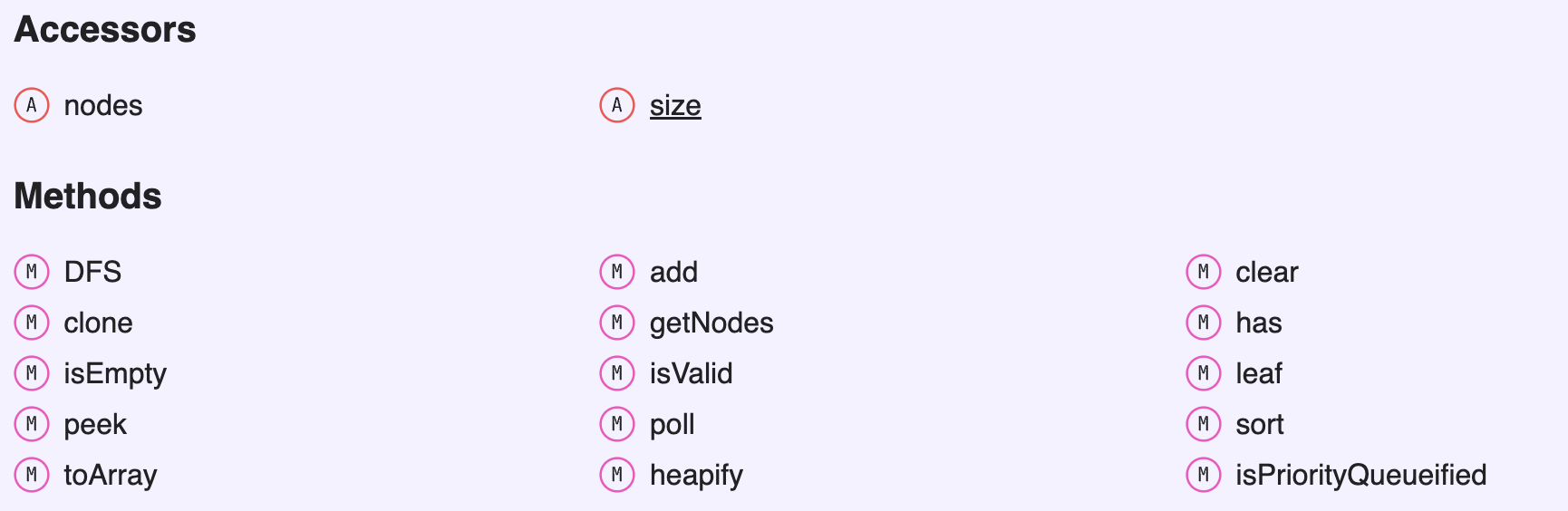Min Priority Queue 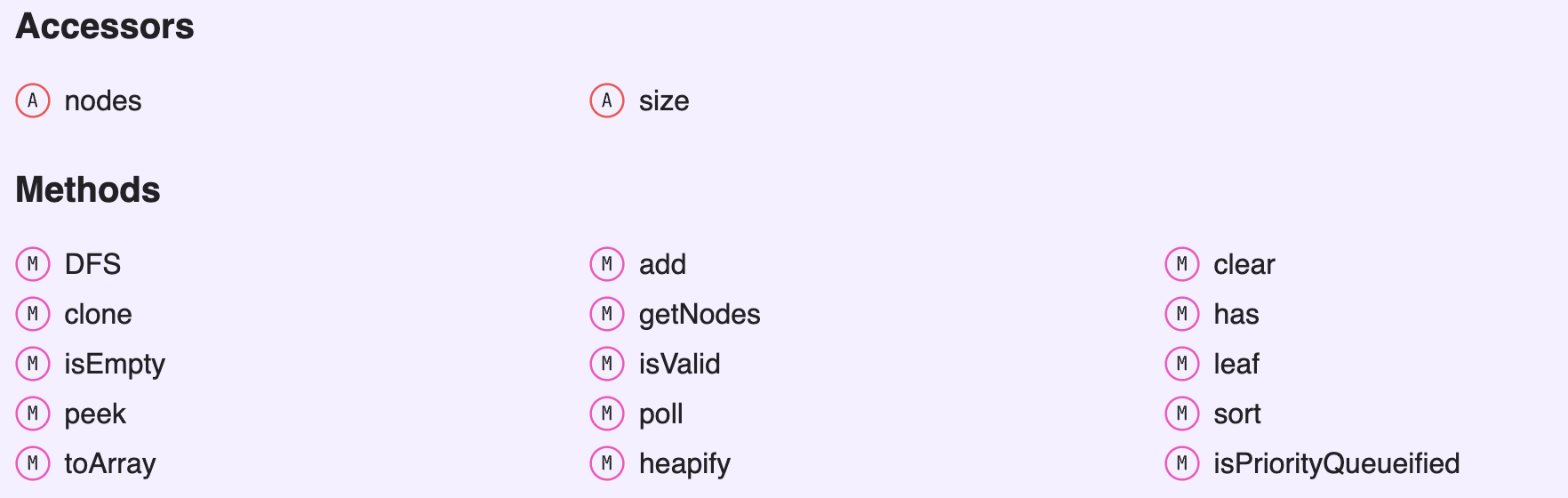Max Priority Queue

snippet

TS

    import {PriorityQueue, MinPriorityQueue} from 'data-structure-typed';
    // /* or if you prefer */ import {PriorityQueue, MinPriorityQueue} from 'priority-queue-typed';

    const minPQ = new PriorityQueue<number>({nodes: [5, 2, 3, 4, 6, 1], comparator: (a, b) => a - b});
    minPQ.toArray()             //  [1, 2, 3, 4, 6, 5]
    minPQ.poll();
    minPQ.poll();
    minPQ.poll();
    minPQ.toArray()             //  [4, 5, 6]
    minPQ.peek()                //  4
    PriorityQueue.heapify({
        nodes: [3, 2, 1, 5, 6, 7, 8, 9, 10],
        comparator: (a, b) => a - b
    }).toArray()                //  [1, 2, 3, 5, 6, 7, 8, 9, 10]

    const priorityQueue = new MinPriorityQueue<number>();
    priorityQueue.add(5);
    priorityQueue.add(3);
    priorityQueue.add(7);
    priorityQueue.add(1);
    const sortedArray = priorityQueue.sort(); //  [1, 3, 5, 7]);

    const minPQ1 = new PriorityQueue<number>({nodes: [2, 5, 8, 3, 1, 6, 7, 4], comparator: (a, b) => a - b});
    const clonedPriorityQueue = minPQ1.clone();
    clonedPriorityQueue.getNodes()  //  minPQ1.getNodes()
    clonedPriorityQueue.sort()      //  [1, 2, 3, 4, 5, 6, 7, 8]
    minPQ1.DFS('in')                //  [4, 3, 2, 5, 1, 8, 6, 7]
    minPQ1.DFS('post')              //  [4, 3, 5, 2, 8, 7, 6, 1]
    minPQ1.DFS('pre')               //  [1, 2, 3, 4, 5, 6, 8, 7]
Copy

JS

    const {PriorityQueue, MinPriorityQueue} = require('data-structure-typed');
    // /* or if you prefer */ const {PriorityQueue, MinPriorityQueue} = require('priority-queue-typed');

    const minPQ = new PriorityQueue({nodes: [5, 2, 3, 4, 6, 1], comparator: (a, b) => a - b});
    minPQ.toArray()             //  [1, 2, 3, 4, 6, 5]
    minPQ.poll();
    minPQ.poll();
    minPQ.poll();
    minPQ.toArray()             //  [4, 5, 6]
    minPQ.peek()                //  4
    PriorityQueue.heapify({
        nodes: [3, 2, 1, 5, 6, 7, 8, 9, 10],
        comparator: (a, b) => a - b
    }).toArray()                //  [1, 2, 3, 5, 6, 7, 8, 9, 10]
    
    const priorityQueue = new MinPriorityQueue();
    priorityQueue.add(5);
    priorityQueue.add(3);
    priorityQueue.add(7);
    priorityQueue.add(1);
    const sortedArray = priorityQueue.sort(); //  [1, 3, 5, 7]);
    
    const minPQ1 = new PriorityQueue<number>({nodes: [2, 5, 8, 3, 1, 6, 7, 4], comparator: (a, b) => a - b});
    const clonedPriorityQueue = minPQ1.clone();
    clonedPriorityQueue.getNodes()  //  minPQ1.getNodes()
    clonedPriorityQueue.sort()      //  [1, 2, 3, 4, 5, 6, 7, 8]
    minPQ1.DFS('in')                //  [4, 3, 2, 5, 1, 8, 6, 7]
    minPQ1.DFS('post')              //  [4, 3, 5, 2, 8, 7, 6, 1]
    minPQ1.DFS('pre')               //  [1, 2, 3, 4, 5, 6, 8, 7]
Copy

API docs & Examples

API Docs

Live Examples

Examples Repository

Data Structures

Data Structure	Unit Test	Performance Test	API Documentation	Implemented
Binary Tree			Binary Tree
Binary Search Tree (BST)			BST
AVL Tree			AVLTree
Tree Multiset			TreeMultiset
Segment Tree			SegmentTree
Binary Indexed Tree			BinaryIndexedTree
Graph			AbstractGraph
Directed Graph			DirectedGraph
Undirected Graph			UndirectedGraph
Linked List			SinglyLinkedList
Singly Linked List			SinglyLinkedList
Doubly Linked List			DoublyLinkedList
Queue			Queue
Object Deque			ObjectDeque
Array Deque			ArrayDeque
Stack			Stack
Coordinate Set			CoordinateSet
Coordinate Map			CoordinateMap
Heap			Heap
Priority Queue			PriorityQueue
Max Priority Queue			MaxPriorityQueue
Min Priority Queue			MinPriorityQueue
Trie			Trie

Why

Complexities

performance of Big O

Big O Notation	Type	Computations for 10 elements	Computations for 100 elements	Computations for 1000 elements
O(1)	Constant	1	1	1
O(log N)	Logarithmic	3	6	9
O(N)	Linear	10	100	1000
O(N log N)	n log(n)	30	600	9000
O(N^2)	Quadratic	100	10000	1000000
O(2^N)	Exponential	1024	1.26e+29	1.07e+301
O(N!)	Factorial	3628800	9.3e+157	4.02e+2567

Data Structure Complexity

Data Structure	Access	Search	Insertion	Deletion	Comments
Array	1	n	n	n
Stack	n	n	1	1
Queue	n	n	1	1
Linked List	n	n	1	n
Hash Table	-	n	n	n	In case of perfect hash function costs would be O(1)
Binary Search Tree	n	n	n	n	In case of balanced tree costs would be O(log(n))
B-Tree	log(n)	log(n)	log(n)	log(n)
Red-Black Tree	log(n)	log(n)	log(n)	log(n)
AVL Tree	log(n)	log(n)	log(n)	log(n)
Bloom Filter	-	1	1	-	False positives are possible while searching

Sorting Complexity

Name	Best	Average	Worst	Memory	Stable	Comments
Bubble sort	n	n2	n2	1	Yes
Insertion sort	n	n2	n2	1	Yes
Selection sort	n2	n2	n2	1	No
Heap sort	n log(n)	n log(n)	n log(n)	1	No
Merge sort	n log(n)	n log(n)	n log(n)	n	Yes
Quick sort	n log(n)	n log(n)	n2	log(n)	No	Quicksort is usually done in-place with O(log(n)) stack space
Shell sort	n log(n)	depends on gap sequence	n (log(n))2	1	No
Counting sort	n + r	n + r	n + r	n + r	Yes	r - biggest number in array
Radix sort	n * k	n * k	n * k	n + k	Yes	k - length of longest key